注:本文的主要内容是在已知样本的先验概率和类条件分布的情况下,寻找最优的决策规则的问题,并不涉及样本类条件密度的估计。
统计决策方法的思想是对数据总体建立概率模型,通过估计数据属于不同类别的后验概率来进行分类决策。
贝叶斯决策是统计决策方法的一种,它通过贝叶斯公式将后验概率比较的问题转化为类条件概率(密度)比较的问题,后者更容易估计。
最小错误率贝叶斯决策
目标函数
最小化总错误率(所有独立同分布样本上错误概率的期望):
$$
\min P(e) = \int P(e|x)p(x) dx
$$
其中 \( P(e|x) = 1 - P(\omega_x | x) \),\( \omega_x \) 表示 x 的真实类别。所以最小化错误率其实是最大化后验概率 \( P(\omega_x | x) \)。
注意:优化的对象是决策规则,而非概率密度函数中的参数。
决策规则
后验概率大者为决策结果。两类问题上:
$$
\text{若}\ P(\omega_i | x) = \max_j P(\omega_j | x),\ \text{则}\ x \in \omega_i.
$$
根据贝叶斯公式 \( P(\omega_i | x) = \frac{ p(x|\omega_i) P(\omega_i) }{p(x)} \),决策规则有如下几种等价形式:
(1)只需比较分子:
$$
\text{若}\ p(x|\omega_i) P(\omega_i) = \max_j p(x|\omega_j) P(\omega_j),\ \text{则}\ x \in \omega_i.
$$
(2)似然比规则:
$$
\text{若}\ l(x) = \frac{p(x|\omega_1)}{p(x|\omega_2)} > \lambda = \frac{P(\omega_2)}{P(\omega_1)},\ \text{则}\ x \in \omega_1,\ \text{反之同理.}
$$
(3)对数似然比:
$$
\text{若}\ h(x) > \log \frac{P(\omega_1)}{P(\omega_2)},\ \text{则}\ x \in \omega_1,\ \text{反之同理.}
$$
其中对数似然比(注意负号) \( h(x) = -\log [l(x)] = -\log p(x|\omega_1) + \log p(x|\omega_2) \)。
错误率计算
总体错误率等于各个决策区域里错误率的加权和,权值为先验概率:
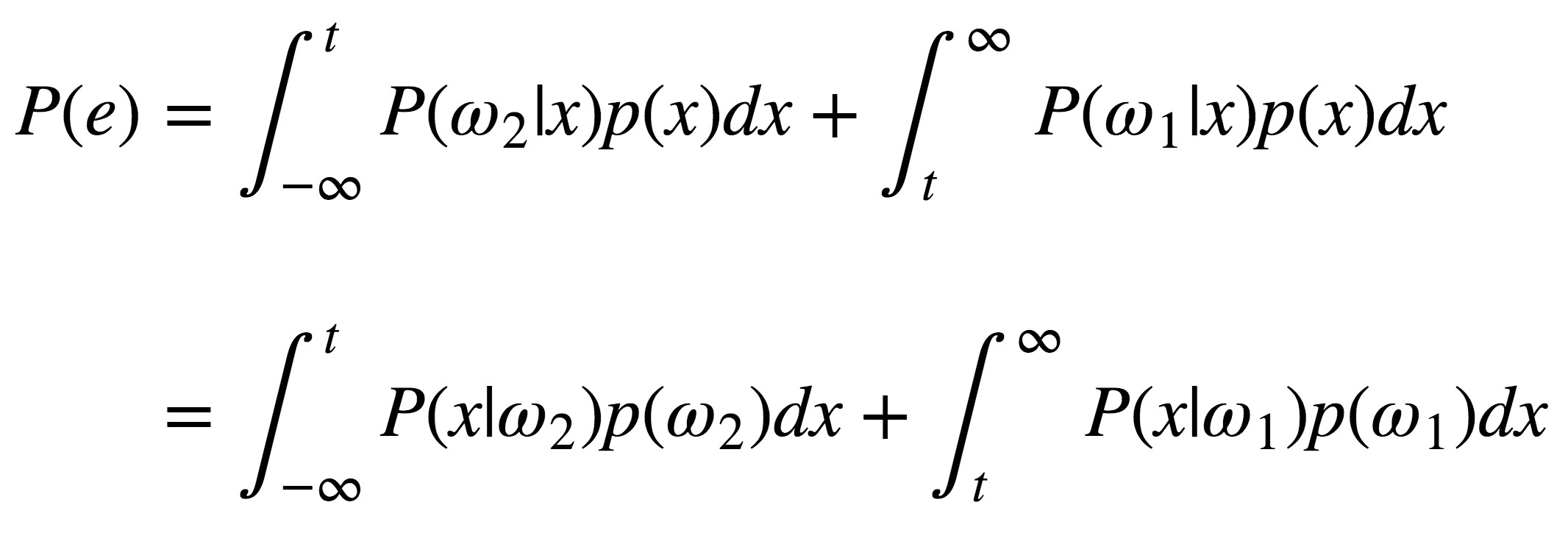
也可以写为:
$$
\begin{equation}\begin{split}
P(e) &= P(x\in \mathcal{R}_1, \omega_1) + P(x\in \mathcal{R}_2, \omega_2) \\
&= P(\omega_2) P_2(e) + P(\omega_1) P_1(e)
\end{split}\end{equation}
$$
多类别决策中可以通过计算平均正确率来得到错误率:
$$
\begin{equation}\begin{split}
P(c) &= \sum_{j=1}^c P(x\in \mathcal{R}_j | \omega_j)P(\omega_j) \\
P(e) &= 1 - P(c)
\end{split}\end{equation}
$$
最小风险贝叶斯决策
目标函数
最小化所有样本上的期望损失:
$$
\min_{\alpha} R(\alpha) = \int R(\alpha(x) | x) p(x) dx.
$$
其中 \(\alpha(x)\) 为决策规则,且
$$
R(\alpha_i|x) = E(\lambda(\alpha_i,\omega_j)|x) = \sum_j \lambda(\alpha_i,\omega_j)P(\omega_j|x).
$$
注意:优化的对象是决策规则 \(\alpha(x)\),而非概率密度函数中的参数。
决策规则
选择风险最小的作为决策结果:
$$
\text{若}\ R(\alpha_i|x) = \min_j R(\alpha_j|x),\ \text{则}\ \alpha = \alpha_i.
$$
在两类问题中,等价于:
$$
\text{若}\ \lambda(1,1) P(\omega_1|x) + \lambda(1,2) P(\omega_2|x) > \lambda(2,1)P(\omega_2|x) + \lambda(2,2) P(\omega_2|x),\ \text{则}\ x \in \omega_1,\ \text{反之同理}.
$$
即:
$$
\text{若}\ l(x) = \frac{p(x|\omega_1)}{p(x|\omega_2)} > \frac{P(\omega_2)}{P(\omega_1)} \cdot \frac{\lambda(1,2) - \lambda(2,2)}{\lambda(2,1) - \lambda(1,1)},\ \text{则}\ x \in \omega_1,\ \text{反之同理}.
$$
决策过程
(1)利用贝叶斯公式计算后验概率;
(2)参考决策表,计算条件风险 \(R(\alpha_i|x) = \sum_j \lambda(\alpha_i,\omega_j)P(\omega_j|x)\)。(\(R(\alpha_i|x) \) 的理解:把 x 属于各个类别的后验概率,分别乘以这些类别判断为第 i 类的风险,求和即为把 x 判断为第 i 类的风险);
(3)选择风险最小的作为决策结果。
Neyman-Pearson 决策规则
固定一类错误率,尽可能最小化另一类错误率:
$$
\begin{equation}\begin{split}
\min & P_1(e) \\
\text{s.t.} & P_2(e) - \epsilon_0 = 0
\end{split}\end{equation}
$$
通过拉格朗日乘子法转化为:
$$
\min \gamma = P_1(e) + \lambda (P_2(e) - \epsilon_0)
$$
优化对象是决策边界。令 \(\gamma\) 对 \(\lambda\) 求导置零可得,在决策边界上应该满足:
$$
\lambda = \frac{p(x|\omega_1)}{p(x|\omega_2)}
$$
于是,决策规则是:
$$
\text{若}\ l(x) = \frac{p(x|\omega_1)}{p(x|\omega_2)} > \lambda,\ \text{则}\ x \in \omega_1,\ \text{反之同理.}
$$
其中 \(\lambda\) 是使约束满足的一个阈值。
总结
相关概念
- 先验概率、后验概率、贝叶斯公式,最小错误率准则,类条件密度,贝叶斯决策,总体错误率;
- 似然比、对数似然比,决策边界、分类线、决策面、分类面;
- 决策论:(1)样本:随机向量;(2)状态空间 \(\Omega\);(3)决策空间 \(\mathcal{A}\);(4)损失函数(决策表 \(\lambda(\alpha_i, \omega_j)\),需要人为确定);条件风险;
- 真阳性、真阴性、假阳性(误报)、假阴性(漏报),灵敏度、特异度,第一类错误(率)、第二类错误(率);
- ROC 曲线(似然比阈值从 0 到 1 的假阳性/真阳性曲线),AUC 准则。
理解
- 最小风险贝叶斯决策实际就是通过定义两类错误(假阳性、假阴性)不同的相对损失来取得二者之间的折中。
- 注意:本文所述的三种决策方法中,优化的对象都是决策规则,而非概率模型中的参数。参数优化需待到后文概率密度函数估计中解释。
计算
- 先验概率:先验概率通过不同类别中样本出现次数比例得到。
- 总体错误率:按照决策边界把样本空间划分为 c 个决策区域,计算每个区域里的错误率,根据先验概率加权求和。多类情况下错误率可以通过 (1 - 正确率) 得到。
比较
- 本文所述三种方法的决策规则,区别仅仅在于对似然比设定的阈值不同。