CNN 简史与 Keras 增量实现

发表于   |   分类于   |     |   阅读次数

本文从最早的 LeNet，到后来的 AlexNet, GoogLeNet，再到最新的 ResNet, DNet 等逐步简单介绍 CNN 的发展与理念，并基于 Keras 逐步增量地实现。当然在此之前，我们先实现一个 Softmax 分类器与传统 MLP 神经网络作为 baseline。

准备知识

数据库

我们基于几个基本数据库来验证算法：MNIST 手写字体数据集，CIFAR10 与 CIFAR100 图像分类数据集。

使用 keras 的 datasets 模块来方便地导入数据库：

1
2
3
4
5
6
7
8
9
10
from keras.datasets import mnist, cifar10, cifar100
# mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# cifar10
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
# cifar100
(X_train, y_train), (X_test, y_test) = cifar100.load_data(label_mode='fine')

第一次运行时会自动从网站下载数据库到本地的 ~/.keras/datasets 路径下。导入的数据为 numpy array 类型。可以看看它们的尺寸和数据类型：

1
2
print X_train.shape, y_train.shape, X_test.shape, y_test.shape
print X_train.dtype, y_train.dtype, X_test.dtype, y_test.dtype

MNIST 图片大小为 28x28，共有 10 个类别（数字 0 到 9 的手写字体），训练集共有 60000 张图片，测试集共有 10000 张图片。

CIFAR10 共有 10 类图像，每个图像大小为 32x32x3，训练集有 50000 幅图片，测试集有 10000 幅图片。

CIFAR100 图像数目与大小和 CIFAR10 相同，但它的图像包括 100 个类别（所以平均每个类别只有 500+100 幅图）。

三种数据库的数据类型都是 uint8，标签（y_train 和 y_test）的数据类型为 int64。

机器学习算法结构

机器学习算法通常由三部分组成：得分函数（score function）、损失函数（loss function）和优化算法（optimization）。

得分函数定义了模型结构，例如线性分类器、核分类器和神经网络就属于完全不同的模型结构。

相同的模型结构，不同的损失函数也可能定义截然不同的算法模型。例如，线性回归和支持向量机（SVM）的得分函数都是 \(y = w^T x + b\)，但线性回归的损失函数是最小平方误差（MSE），而支持向量机的损失函数是合页损失（hinge loss），二者的作用和效果完全不同。

常见算法的得分函数、损失函数和优化算法如下：

算法名称 得分函数 损失函数 优化算法
线性回归 \( y = w^T x + b \) MSE: \( \sum_i (y_i - (w^T x + b))^2\) LS 闭合解
SVM \(y = w^T x + b\) hinge loss: \(\sum_i \max(0, 1 - t \cdot y_i\)) SMO, QP, LS
逻辑回归 \(y = \frac{1}{1 + \exp{(-w^T x)}}\) cross entropy loss: \(\sum_i p_i \log (q_i) \) 梯度下降，L-BFGS
MLP 多层神经网络 cross entropy loss: \(\sum_i p_i \log (q_i)\) 反向传播

其中 MLP 的得分函数为：\(y = \sigma ( W_L \cdot … \sigma(W_2 \cdot \sigma( W_1 x + b_1) + b_2) … + b_L )\)。

CNN、RNN 等复杂模型同样由以上三部分组成，但它们的得分函数（亦即其网络结构）更为复杂。它们的损失函数通常包括交叉熵（cross entropy）、MSE 等，其优化算法主要是反向传播。

所以要实现一个机器学习算法，主要需要实现三部分内容：定义得分函数，定义损失函数，实现优化算法。

下面开始进入正题。

CNN 简史与 Keras 增量实现

Softmax 分类器

在学习 CNN 之前，我们先实现一个 Softmax 多类分类器，作为 baseline。

实现 Softmax 过程中涉及的参数初始化、梯度下降和一些实验观察有助于后面对神经网络的理解。Softmax 属于多类分类器，输入为样本特征，输出为样本属于各个类别的概率。

上一节我们提到，机器学习算法通常由三部分组成：得分函数、损失函数和优化算法。我们逐一实现 Softmax 的这几个部分。

得分函数

Softmax 的得分函数输出样本属于不同类别的概率，通过如下公式计算：

$$ p_k = \frac{ \exp{ (w_k^T x) }}{ \sum_j \exp{(w_j^T x)} } $$

\(p_k\) 表示样本 x 属于第 k 个类别的概率，\( \sum_j w_j^T x \) 是归一化项，为了使概率之和为 1。完整的 \(p\) 是 \(C \times 1\) 的向量（\(C\) 是类别个数）。

代码实现如下：

1
2
3
4
def softmax_score(X, W):
    p = np.exp(W.T.dot(X))
    p = p / np.sum(p, axis=0)
    return p

这里用矩阵乘法同时计算出所有样本属于所有类别的概率。

写下各个变量的维度有助于理解。假设有 N 个样本，特征为 D 维，C 个类别，则各变量的维度如下：

$$
X \in \mathbb{R}^{D \times N},
W \in \mathbb{R}^{D \times C},
p \in \mathbb{R}^{C \times 1}
$$

损失函数

Softmax 以交叉熵（cross entropy）定义损失函数。假设样本 x 属于各个类别的真实概率为 \(q = [0,\cdots,1,\cdots,0]\) （在真实类别位置概率为 1，其余位置为 0），估计概率为 p，则 p 与 q 之间的交叉熵定义为：

$$
h = - \sum_{k=1}^C q_k \log (p_k)
$$

损失函数定义为所有样本的交叉熵之和：

$$ J = - \frac{1}{N} \sum_{i,k}^{N,C} q_k^{(i)} \log (p_k^{(i)}) $$

注意到 \( q^{(i)} \) 仅在类别 \(y^{(i)} = k\) 处才为 1，所以损失函数可以写为：

$$ J = - \frac{1}{N} \sum_{i,k}^{N,C} \text{sgn}(y_i == k) \log (p_k^{(i)}) $$

可以这么直观地理解：Softmax 的损失函数就是所有样本在正确类别上概率的 log 和的相反数。

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
def softmax_loss(X, y, W):
    N = X.shape[1]
    C = len(np.unique(y))
    
    p = softmax_score(X, W)
    
    loss = 0
    for k in range(C):
        loss += - np.sum(np.log(p[k,y==k])) / N
    
    return loss

优化算法

损失函数 J 是凸函数，我们使用梯度下降来求得参数 W 的最优解。

首先看看梯度怎么计算。

梯度计算

损失函数 J 是所有样本正确分类的概率的 log 和的相反数，我们可以把它展开为：

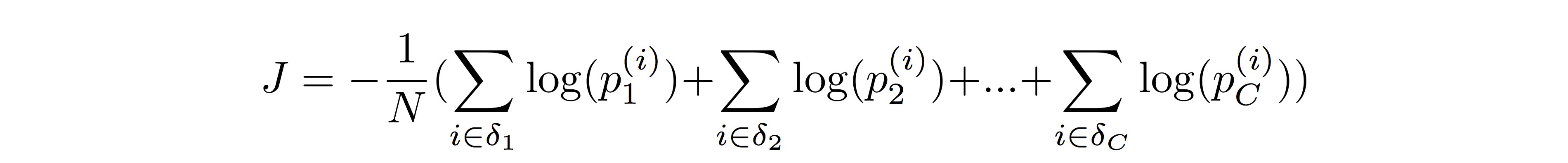
其中 \(\delta_k = \{ i\; |\; y_i = k \} \)。所以要求解 J 对 \(w_k\) 的梯度，我们只需要推导两个梯度公式：

$$
\frac{\partial \log (p_k^{(i)})}{\partial w_k} = x_k (1 - p_k^{(i)})
$$

与

$$
\frac{\partial \log (p_l^{(i)})}{\partial w_k} = - x_k p_k^{(i)},\; l \neq k
$$

\(\nabla_{w_k} J\) 可以表示为许多以上两项的和。求和之后可以得到十分简洁的梯度公式：

$$
\nabla_{w_k} J = -\frac{1}{N} \sum_i x^{(i)} (\text{sgn}(y_i == k)\cdot 1 - p_k^{(i)})
$$

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
def softmax_grad(X, y, W):
    N = X.shape[1]
    C = len(np.unique(y))
    
    p = softmax_score(X, W)
    
    dW = np.zeros_like(W)
    for k in range(C):
        t = (y==k).astype('uint') - p[k,:]
        dW[:,k] = - np.sum(X_train * t, axis=1) / N
    
    return dW

梯度下降

梯度下降的优化过程如下：首先赋予参数 W 一个初始值，可以是随机数或者零；然后计算损失函数 J 在 W 位置的梯度 \(\Delta W\)；接着将 W 沿着梯度的反方向移动一个步长（\(W - \eta \Delta W → W\)）；迭代梯度计算与移动的过程直到损失函数几乎不再变化为止。

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def softmax_train(X, y):
    (D, N) = X.shape
    C = len(np.unique(y))
    
    step = 5e-01
    eps = 1e-03
    
    W = np.zeros((D, C))
    
    loss = 1e10
    last_loss = 0
    
    while np.abs(loss - last_loss) > eps:
        dW = softmax_grad(X, y, W)
        W -= step * dW
        last_loss = loss
        loss = softmax_loss(X, y, W)
        print 'loss:', loss
        
    return W

注意事项

优化过程看起来并不复杂，但有两点需要注意：

一是 W 的初始化。常用的方法是使用随机数初始化，但在 Softmax 里要注意，这个随机数要设得非常小（比如 W = np.random.rand(D, C) * 1e-05）。因为 \(w_k^T x\) 需要经过指数函数映射，如果 W 稍微设大，将会导致指数函数值为 inf，从而概率 p 有可能为 nan。

在 Softmax 里，W 是可以初始化为零矩阵的（并不代表其他算法可以）。这样指数函数值为 1，不会导致数值运算问题，同时样本属于各个类别的概率均等，为 1/C。

二是步长的设置。过大的步长将导致损失函数无法收敛甚至发散，过小的步长导致优化速度太慢，通过观察损失函数的变化可以获知步长设置得是否合适。此外，对于数值范围不同的样本，其步长也要设置得不同。例如像素值 0~255 的图像，需要设置 1e-05 左右的步长，而像素值 0~1 的图像可能只需要 0.5 就可以。

所以为了算法能通用，对数据做归一化的预处理也是很必要的。

测试算法

我们写一个测试函数来评估 Softmax 在测试集上的准确率：

1
2
3
4
5
6
7
def softmax_test(X, y, W):
    p = softmax_score(X, W)
    y_pred = np.argmax(p, axis=0)
    
    acc = np.sum((y_pred==y)) * 1.0 / len(y)
    
    return acc

完整代码

建议大家在一开始实现的时候不要定义太多函数，这样不方便调试和观察变量，最好把代码都写在一个主函数里，容易快速找出问题。

以下是 Softmax 写在一起的完整代码，如果你已经配置过 numpy 与 keras，可以直接运行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# SOFTMAX - ALL IN ONE
from keras.datasets import mnist
import numpy as np
# load data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape((X_train.shape[0], np.product(X_train.shape[1:]))).T / 255.0
X_test = X_test.reshape((X_test.shape[0], np.product(X_test.shape[1:]))).T / 255.0
# parameters
(D, N) = X_train.shape
C = len(np.unique(y_train))
eps = 1e-03
step = 0.5
# init W
W = np.zeros((D, C))
p = np.exp(W.T.dot(X_train))
p /= np.sum(p, axis=0)
# optimization
loss = 1e10
last_loss = 0
while np.abs(loss - last_loss) > eps:
    # compute gradient
    dW = X_train.dot(p.T) / N
    for k in range(C):
        dW[:,k] -= np.sum(X_train[:,y_train==k], axis=1) / N
        
    # gradient descent
    W -= step * dW
    
    # compute loss
    p = np.exp(W.T.dot(X_train))
    p /= np.sum(p, axis=0)
    
    last_loss = loss
    loss = 0
    for k in range(C):
        loss += - np.sum(np.log(p[k,y_train==k])) / N
    print 'Loss:', loss
        
# test
p = np.exp(W.T.dot(X_test))
p /= np.sum(p, axis=0)
y = np.argmax(p, axis=0)
acc = np.sum(y==y_test) * 1.0 / len(y)
print 'Accuracy:', acc

最后输出的准确率为：

1
Accuracy: 0.8981

把数据集换成 cifar10（参数：step=0.01, eps=1e-04 ）或 cifar100（参数：xxx）测试，可分别测得准确率为 0.xxx 和 0.xxx，但是收敛速度比 MNIST 要慢得多。

可见，仅仅基于像素特征，像 Softmax 这样的线性分类器还难以胜任自然图像分类的任务。

观察权值

OK，到目前为止我们已经实现了 Softmax 分类器，并测试了结果。但是，不要着急离开，我们好好研究一下，Softmax 到底学习了什么样的模型。

Softmax 是一个线性分类器，\(w_k\) 的维度与样本 x 的维度一致。我们可以把它以图片的形式显示出来。比如显示用于分类数字 2 的权值：

1
2
3
4
import matplotlib.pyplot as plt
number = 2
plt.imshow(W[:,number].reshape([28, 28]), cmap ='gray')

将会输出如下图像：

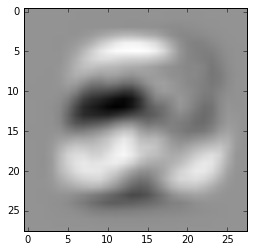
Weight vector for number 2 learned by softmax

我们发现这个权值看起来就是数字 2 的手写字体。白色部分代表大的权值，黑色部分代表小的或者负的权值。所以 \(w_2\) 其实是想要给数字 2 形状部分的像素更大的权值，而惩罚不在形状 2 上但负样本（如 1, 3, 5 等）可能出现的那些位置（比如 2 中间那一片黑色）。

另一方面，我们可以也可以把 \(w_2\) 看成是学习到的数字 2 的一个模板，通过内积运算来进行模板匹配。

为了验证这一点，我们再来看看在 W 的学习过程中发生了什么。\(w_k\) 初始值为零，在梯度下降中，\(w_k\) 每次迭代都加上一个 \((- \Delta w_k)\)，后者的形式如下：

$$
-\nabla_{w_k} J = \frac{1}{N} \sum_i x^{(i)} (\text{sgn}(y_i == k)\cdot 1 - p_k^{(i)})
$$

所以，权值 \(w_k\) 实际上是所有样本的加权和，且同类样本的权值为正（\(1-p_k\)），当概率小时算法以更大的权值去加上这个样本，而不同类样本的权值为负（\(p_k\)），当概率大时算法以更大的权值减去这个样本。最后生成了上图所示的“模板”。

欺骗 Softmax

我们按照数字 2 的权值图像上亮的地方，用画图工具写一个数字 5，看看算法是否真的会把它识别成 2。

画图工具手写的数字 5 与对比模板 2：

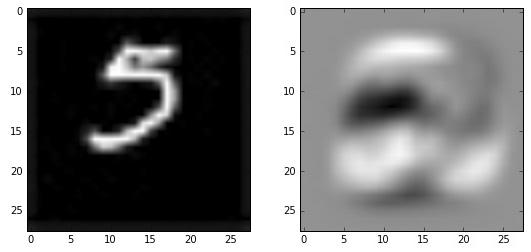
Number 5

代码如下：

1
2
3
4
5
6
7
x = plt.imread('1.5.jpg')  # generated by Photoshop
plt.imshow(x, cmap='gray')
x = (x / 255.0).reshape((28*28,1))
p = np.exp(W.T.dot(x))
p /= np.sum(p, axis=0)
print 'predicted to be:', np.argmax(p)

果然，最后的输出结果是：

1
predicted to be: 2

多层感知机

上一节讲到的 Softmax 属于线性分类器，相当于在特征空间里学习多个超平面将不同类别的样本划分开。

然而，实际应用中的许多数据并非线性可分。多层感知机（Multi-Layer Perceptron, MLP）通过层次模型学习特征到类别之间的非线性映射。

MLP 简史

同样，MLP 由得分函数、损失函数和优化算法三部分构成。

得分函数

MLP 的得分函数亦即其模型结构如下图所示：

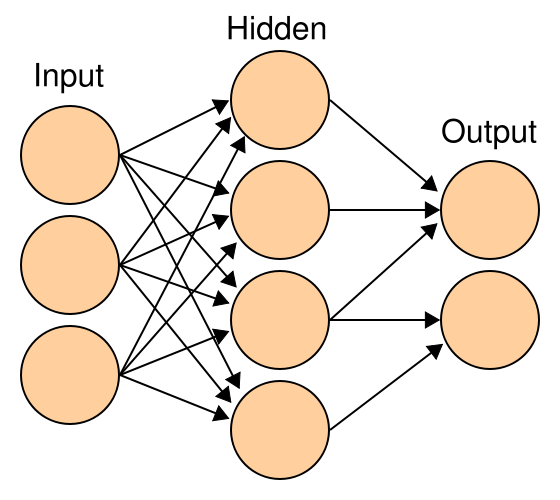
每个节点表示一个神经元，它接受多个输入值，经过线性组合与激活函数的非线性映射后输出一个值。上一层的输出是下一层的输入。隐层神经元的激活函数通常为 Sigmoid 函数，输出层的激活函数可以是 Sigmoid（两类）或 Softmax（多类）等。

MLP 的得分函数用数学表达式可表示如下：

$$
p = \text{softmax} ( W_L \cdot … \sigma(W_2 \cdot \sigma( W_1 x + b_1) + b_2) … + b_L )
$$

其中 \(\sigma(\cdot)\) 表示 Sigmoid 函数 \(\sigma(x) = \frac{1}{1 + \exp(-x)}\)。

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
def mlp_score(X, W):
    L = len(W)  # W is a list of numpy array
    
    input = X
    for l in range(L-1):
        input = 1 / (1 + np.exp(W[l].T.dot(input)))
    
    p = np.exp(W[L].T.dot(input))
    p = p / np.sum(p, axis=0)
    return p

列出各个变量的维度如下：

$$
X \in \mathbb{R}^{D \times N},
W_1 \in \mathbb{R}^{D \times M_1},
W_2 \in \mathbb{R}^{M_1 \times M_2},
\cdots,
p \in \mathbb{R}^{C \times 1}
$$

其中 N 为样本个数，D 为特征维度，神经网络为 L+1 层，除去输出层外，每层各有 \(M_1,\; M_2,\;\cdots,\; M_L\) 个节点。

损失函数

与 Softmax 一样，这里使用交叉熵作为损失函数：

$$ J = - \frac{1}{N} \sum_{i,k}^{N,C} q_k^{(i)} \log (p_k^{(i)}) $$

其中 \(q_k^{(i)}\) 表示第 i 个样本属于第 k 个类别的真实概率（0 或 1）。

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
def mlp_loss(X, y, W):
    N = X.shape[1]
    C = len(np.unique(y))
    
    p = mlp_score(X, W)
    
    loss = 0
    for k in range(C):
        loss += - np.sum(np.log(p[k,y==k])) / N
    
    return loss

优化算法

MLP 的优化算法是反向传播。

LeNet-1 ~ LeNet-5

AlexNet

GoogLeNet

VGGNet

ResNet

DNet